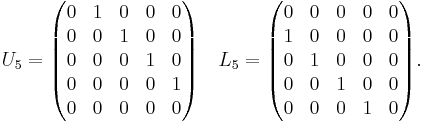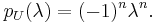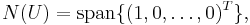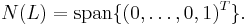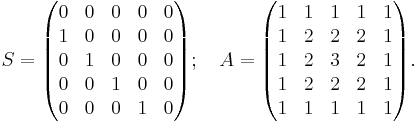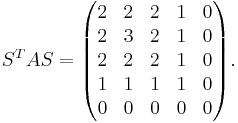Shift matrix

In mathematics, a shift matrix is a binary matrix with ones only on the superdiagonal or subdiagonal, and zeroes elsewhere. A shift matrix U with ones on the superdiagonal is an upper shift matrix. The alternative subdiagonal matrix L is unsurprisingly known as a lower shift matrix. The (i,j):th component of U and L are

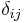$U_{ij} = \delta_{i%2B1,j}, \quad L_{ij} = \delta_{i,j%2B1},$

where $\delta_{ij}$ is the Kronecker delta symbol.

For example, the 5×5 shift matrices are

$U_5=\begin{pmatrix} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 \end{pmatrix} \quad L_5=\begin{pmatrix} 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{pmatrix}.$

Clearly, the transpose of a lower shift matrix is an upper shift matrix and vice versa.

Premultiplying a matrix A by a lower shift matrix results in the elements of A being shifted downward by one position, with zeroes appearing in the top row. Postmultiplication by a lower shift matrix results in a shift left. Similar operations involving an upper shift matrix result in the opposite shift.

Clearly all shift matrices are nilpotent; an n by n shift matrix S becomes the null matrix when raised to the power of its dimension n.

1 Properties
2 Examples
3 See also
4 References

Properties

Let L and U be the n by n lower and upper shift matrices, respectively. The following properties hold for both U and L. Let us therefore only list the properties for U:

det(U) = 0
trace(U) = 0
rank(U) = n−1
The characteristic polynomials of U is

$p_U(\lambda) = (-1)^n\lambda^n.$

Uⁿ = 0. This follows from the previous property by the Cayley–Hamilton theorem.

The permanent of U is 0.

The following properties show how U and L are related:

L^T = U; U^T = L

The null spaces of U and L are

$N(U) = \operatorname{span}\{ (1,0,\ldots, 0)^T \},$

$N(L) = \operatorname{span}\{ (0,\ldots, 0, 1)^T \}.$

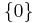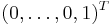The spectrum of U and L is $\{0\}$ . The algebraic multiplicity of 0 is n, and its geometric multiplicity is 1. From the expressions for the null spaces, it follows that (up to a scaling) the only eigenvector for U is $(1,0,\ldots, 0)^T$ , and the only eigenvector for L is $(0,\ldots, 0,1)^T$ .

For LU and UL we have

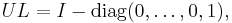
$UL = I - \operatorname{diag}(0,\ldots, 0,1),$

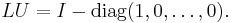
$LU = I - \operatorname{diag}(1,0,\ldots, 0).$

These matrices are both idempotent, symmetric, and have the same rank as U and L

L^n-aU^n-a + L^aU^a = U^n-aL^n-a + U^aL^a = I (the identity matrix), for any integer a between 0 and n inclusive.

Examples

$S=\begin{pmatrix} 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{pmatrix}; \quad A=\begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 1 & 2 & 2 & 2 & 1 \\ 1 & 2 & 3 & 2 & 1 \\ 1 & 2 & 2 & 2 & 1 \\ 1 & 1 & 1 & 1 & 1 \end{pmatrix}.$

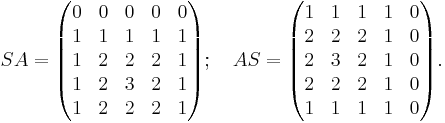
Then $SA=\begin{pmatrix} 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 2 & 2 & 2 & 1 \\ 1 & 2 & 3 & 2 & 1 \\ 1 & 2 & 2 & 2 & 1 \end{pmatrix}; \quad AS=\begin{pmatrix} 1 & 1 & 1 & 1 & 0 \\ 2 & 2 & 2 & 1 & 0 \\ 2 & 3 & 2 & 1 & 0 \\ 2 & 2 & 2 & 1 & 0 \\ 1 & 1 & 1 & 1 & 0 \end{pmatrix}.$

Clearly there are many possible permutations. For example, 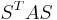$S^{T}AS$ is equal to the matrix A shifted up and left along the main diagonal.

$S^{T}AS=\begin{pmatrix} 2 & 2 & 2 & 1 & 0 \\ 2 & 3 & 2 & 1 & 0 \\ 2 & 2 & 2 & 1 & 0 \\ 1 & 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{pmatrix}.$

References

Shift Matrix - entry in the Matrix Reference Manual

Shift matrix

Contents

Properties

Examples

See also

References